『二重人格探偵エリザ 嗤う双面神』( isbn:9784596550255 )
『二重人格探偵エリザ 嗤う双面神』は、ヴィクトリア朝ロンドンが舞台の小説です。例えば、こんなふうに紹介することもできるでしょう。「ようやくスコットランドヤードに科学捜査が入り始めたこの時期、女性警察医エリザ・ジキルは周囲の偏見に苦しみながら科学の力で連続殺人鬼に挑む！」とかなんとか。
それもまたこの小説の一面ではありますけど、いや、まったくもう、素晴らしくいかがわしい小説でした！ 昼は王立協会の捜査官が錬金術師を連行するべくあちこちに顔を出し、夜は連続殺人鬼が暗がりで人を襲うんですよ。科学と錬金術と殺人！
バングラデシュ時間で過ごしました
ちょっと前のことなのですが、起きた時を7時に設定して暮らす、という話をtwitterで読みました。
昼夜逆転を直すのを諦めて、起きた時間にアナログ時計を七時にセットして 一日その時計にあわせて生活してみるという方法を試しているところなのですが それによると今はわたし時間の夜十二時で、ものすごく眠い。朝七時に起きると夜十二時ってこんなに眠いものなんだなあ。
— おみおみ_君が死なない日のごはん (@omiomi_kekyu) 2016年4月4日
人と会う予定の無い日を選んで、これを試してみたのです。10時（JST）に起きたので、3時間の時差。これがどこの標準時かと調べてみたら、バングラデシュ時間でした。浮き稲の国ですね。
時計をいじって今日はJST-3にしました。バングラデシュあたり。そろそろお昼です
— Lucas KBYS (@lkbys) 2016年5月20日
「そろそろお昼です」などと書いていますが、実はこのとき精神的にダメージを負っていました。設定してから約5時間。時計はそろそろお昼だと主張しているのに、窓の外では日が傾きかけているのです。世界から拒絶されてる感が地味につらい。
この、一人だけちょっとずれた時間で生活してるっていうのSFっぽくてよくないですか……すごく眠いけど……
— おみおみ_君が死なない日のごはん (@omiomi_kekyu) 2016年4月4日
最初の2時間くらいはそう思えて、とても良かったんですけどね……。
何がいけなかったんだろうか、と考えてみると、
- 3時間という時差が半端で良くなかった、
- 洗濯しない日なら太陽を気にせずに済んだ、
- そもそも性格的に向いてない、
- 前日に「漂った男」（小川一水）を読んでいたのが効いた、
などが原因として挙げられるところです。「漂った男」のせいにしておきたい。
ねこあつめはじめました
母や妹が遊んでいるのをちょっと見せてもらっていたので、何となくいろいろ知識のある状態でスタート。
一人暮らしはじめました
深夜に歯ブラシを買いに出るなどしました。
電車からちょっと遠くなりました。
観ました: アナと雪の女王
後半だけ観ました。あとで何か書きます。
虫食い算
今年は1問です。
過去の虫食い算はこちら：
d:id:Koba-L:20120108#p2
d:id:Koba-L:20130112#p2
d:id:Koba-L:20140115#p2
d:id:Koba-L:20150115#p2
今年の虫食い算メイキング
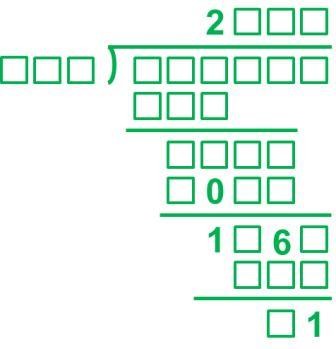
もう11か月も前のことですが、こんな虫食い算を作りました：
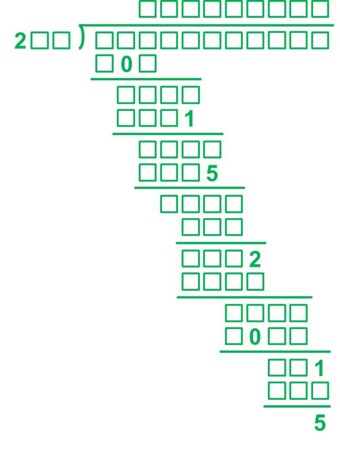
この虫食い算を作る際にどんなことを考えていたのか、書いてみましょう。
なお、答などに触れていますので、ネタバレが嫌な方は解いてから続きを読んでください。
ライズ重日が今年ではなく3年後にあること
ユールとライズ
よく知られているように、ホビット庄暦には12か月に属さない日が存在します。
平年には5日、閏年には6日。そのうち2日が冬（ユール）、残りが夏（ライズ）です。
我々が普段使っているグレゴリオ暦では2月の日数によって閏を入れますが、ホビット庄暦はそうではないのです。
ホビット庄暦の閏年
ホビット庄暦の平年の夏には、夏至とその前後の計3日間が、12か月に属さない日となります。
一方、閏年なら、夏至の後をもう1日余計に入れてライズ重日と称するわけです*1。
ライズ重日は盛大に祝うものとされていますから、これがどの年にあるのかを知ることはとても重要です。
さて、今年はライズ重日のある年なのでしょうか？
今年の夏至の日から来年の夏至の日までが366日であるかどうか、調べれば良いですね。この間には2016年2月29日が存在しますから、366日のような気がします。
あるいはもっと一般的に言って、ライズ重日が存在するのは、グレゴリオ暦における閏年の前年なのではないでしょうか？
日本における夏至の日
結論から言ってしまうと、この「ライズ重日が存在するのは、グレゴリオ暦における閏年の前年」は、実は誤りです。表を見てください（時刻はJST）*2：
| 年 | 夏至 |
|---|---|
| 2013 | 6月21日14:04 |
| 2014 | 6月21日19:51 |
| 2015 | 6月22日01:38 |
| 2016 | 6月21日07:34 |
今年2015年の夏至の日が22日であること、来年2016年の夏至の日が21日であることがわかります。来年2月29日が存在するのと差し引きされて、この間365日。平年です。去年がライズ重日だったのですね。
さて、先ほどの表のもう少し上の方を見てみましょう。
| 年 | 夏至 |
|---|---|
| 2000 | 6月21日10:48 |
| 2001 | 6月21日16:38 |
| 2002 | 6月21日22:24 |
| 2003 | 6月22日04:10 |
| 2004 | 6月21日09:57 |
| 2005 | 6月21日15:46 |
| 2006 | 6月21日21:26 |
| 2007 | 6月22日03:06 |
| 2008 | 6月21日08:59 |
2000年には、夏至はJSTで6月21日10:48でした。1年間は365日と6時間弱なので、2001年、2002年、2003年と、夏至の時刻が遅れていきます。2003年にはついに日付を跨いで、22日04:10です。
ところがその翌年2004年には6月21日に戻っています。これは、2003年の夏至と2004年の夏至の間に2月29日が挿入されたことによります。
こうして、夏至は、
- 4の倍数の年は、6月21日の午前中；
- 4で割って1余る年は、前年よりも6時間弱遅い；
- 4で割って2余る年は、前年よりも6時間弱遅い；
- 4で割って3余る年も、前年よりも6時間弱遅く、その結果、6月22日になる；
を繰り返すことになります。
以上を総合すると、
となって、4で割って2余る年にライズ重日が存在するのです。
もっと後の話
さて、ここまでの話を1セット繰り返すと夏至は約45分早まります。4年間は365日×4と23時間15分くらいなのです*3。
2003年には、夏至はJSTで6月22日04:10でした。4時間10分を45分で割ると、5と6の間。6セット繰り返した2027年には、4で割って3余る年の夏至の日は6月21日となります。
また、2000年には、夏至はJSTで6月21日10:48でした。10時間48分を45分で割ると、だいたい14。2056年頃には、4の倍数年の夏至の日は6月20日となります。
……と、25セット繰り返すとほぼ1日分のずれが溜まって、2月が28日しか無い2100年を迎えるわけです。
- 2022年まで、4で割って2余る年にライズ重日。
- 2026年はライズ重日が無い。
- 2027年以降2051年まで、4で割って3余る年にライズ重日。
- 2055年はライズ重日が無い。
- 2056年にライズ重日。
